1. 딥러닝과 머신러닝 차이, 그래서 딥러닝이 뭔데?
2. 로지스틱 회귀 복습
3. 인공신경망에 대해 알아보자
4. 심층 신경망
5. 신경망 모델 훈련
최대한 간단간단하게 하자
머신러닝이 뭐였더라?
머신러닝은 데이터를 구문 분석하고 해당 데이터를 통해 학습한 후 정보를 바탕으로 결정을 내리기 위해 학습한 내용을 적용하는 알고리즘
즉, 주어진 데이터로 기능을 수행하고, 시간이 지남에 따라 그 기능이 점차 향상되는것

그럼 딥러닝은?
딥러닝은 머신러닝의 하위 개념!!으로 인공신경망이라고도 한다
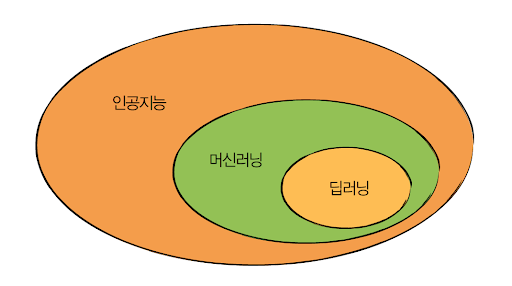
그럼 인공신경망은 뭘까?

우리 뇌에 있는 신경세포인 뉴런을 수학적으로 모델링한 것
인공신경망 뉴런은 뇌의 뉴런처럼 다른 여러개의 뉴런으로부터 입력값을 받아서 외부로 출력값을 내보내는 것이다

저번 시간에 봤던 걸 살펴보자
요약하자면, 패션 MNIST라는 여러 의류들이 있는 데이터셋을 가지고와서 로지스틱 회귀라는 알고리즘이 이 데이터들을 얼마나 정확히 맞힐 수 있는지를 보았다
그때 28*28 픽셀로 이루어진 6만개의 데이터들을 쫘라락 펼쳐서 늘려놓았다
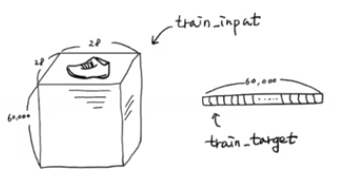
지금 train_target의 네모 한 칸은 28*28 크기의 데이터이다
이걸 파이썬의 reshape라는 함수를 사용해 2차원 배열을 1차원배열로 만들어야한다 ->numpy 계산을 위해
train_scaled = train_scaled.reshape(-1, 28*28)이는 데이터의 높이와 너비를 곱해서 하나의 차원으로 만들어서 각 샘플이 하나의 배열로 되도록 만든다
즉, 28 x 28을 해서 784로 만들겠다는 소리
(60000, 784)그러면 이렇게 784픽셀로 이루어진 6만개의 샘플이 만들어졌음을 볼 수 있다
그리고 우리는 SGDClassifier 클래스라는 로지스틱 회귀를 사용해서 성능을 확인해보았다
from sklearn.model_selection import cross_validate
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log', max_iter=5, random_state=42)
scores = cross_validate(sc, train_scaled, train_target, n_jobs=-1)
print(np.mean(scores['test_score']))그랬더니 정확도가 약 0.82%가 나왔음을 확인했다
이를 그림으로 표현하자면,

이런 식으로 표현할 수 있다. 즉, 픽셀 하나하나에 어떤 가중치와 절편을 곱해서 사용한 것이다
가중치와 절편이라는 소리가 나온 이유?
로지스틱 회귀는 분류 모델이다. 분류는 여러 개의 종류 중 하나를 구별해내는 문제를 말한다. 즉 어떤 데이터를 얼마나 잘 구별하는지 본다는 소리
로지스틱 회귀는
z = a * (Weight) + b * (Length) + c * (Diagonal) + d * (Height) + e * (Width) + f
위와 같은 공식을 사용해서 계산을 한다
여기서 a,b,c,d,e가 가중치고 f가 절편이다.
위 공식을 지금 데이터처럼 바꿔본다면
z_티셔츠 = w1 x (픽셀1) + w2 x (픽셀2) + ... + w784 x (픽셀784) + b
. . .
z_바지 = w1' x (픽셀1) + w2' x (픽셀2) + ... + w784' x (픽셀784) + b'
이런식으로 바꿀 수 있겠다.
즉, 픽셀 하나하나에 어떤 가중치를 곱하고 마지막에 절편이라는 것을 더해서 그 값이 티셔츠인지, 바지인지 맞히는 형식이다
*위와 같은 공식을 '선형 방정식' 이라고 한다*
그럼 이제 인공 신경망에 대해 살펴보자

z1, z2와 같이 출력층이 형성되었는데 이 데이터셋에서 패션아이템이 총 10개가 있었다(티셔츠, 바지, 스웨터, 가방 등 10가지의 종류가 있다고 했었다)
그래서 z10까지 있는 것이고, 신경망의 최종값을 만든다는 의미에서 출력층이라고 부른다.
인공 신경망에서 z값을 계산하는 단위를 뉴런이라고 부른다
그리고 픽셀 1, 픽셀 2를 x1, x2와 같이 바꾸었다. 이 픽셀은 총 784개이니, x784까지 있는 것이다. 이를 입력층이라고 부른다
이 입력층은 픽셀값 자체일 뿐이고 특별한 계산을 하지 않는 층이다
이제 인공 신경망 모델을 만들어보자
from sklearn.model_selection import train_test_split
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state = 42)사이킷런에서 모델을 가지고왔다고 가정하고 훈련세트와 검증세트로 나누었다.
*훈련세트는 훈련을 시키는 애들이고 검증세트는 테스트세트를 사용하기 위해 이 알고리즘이 얼만큼의 성능을 낼 수 있는지 여러번 가늠하기 위해 사용하는 것*
print(train_scaled.shape, train_target.shape)
#훈련세트 크기 : (48000, 784) (48000,)
print(val_scaled.shape, val_target.shape)
#검증세트 크기 : (12000, 784) (12000,)6만개의 데이터 중에 48000개가 훈련세트가 되었고, 12000개가 검증세트가 되었다
케라스의 레이어(keras.layers)라는 패키지 안에는 다양한 층이 준비되어있다.
가장 기본이 되는 층은 밀집층(dense layer)이다
왜 밀집이라고 부를까?
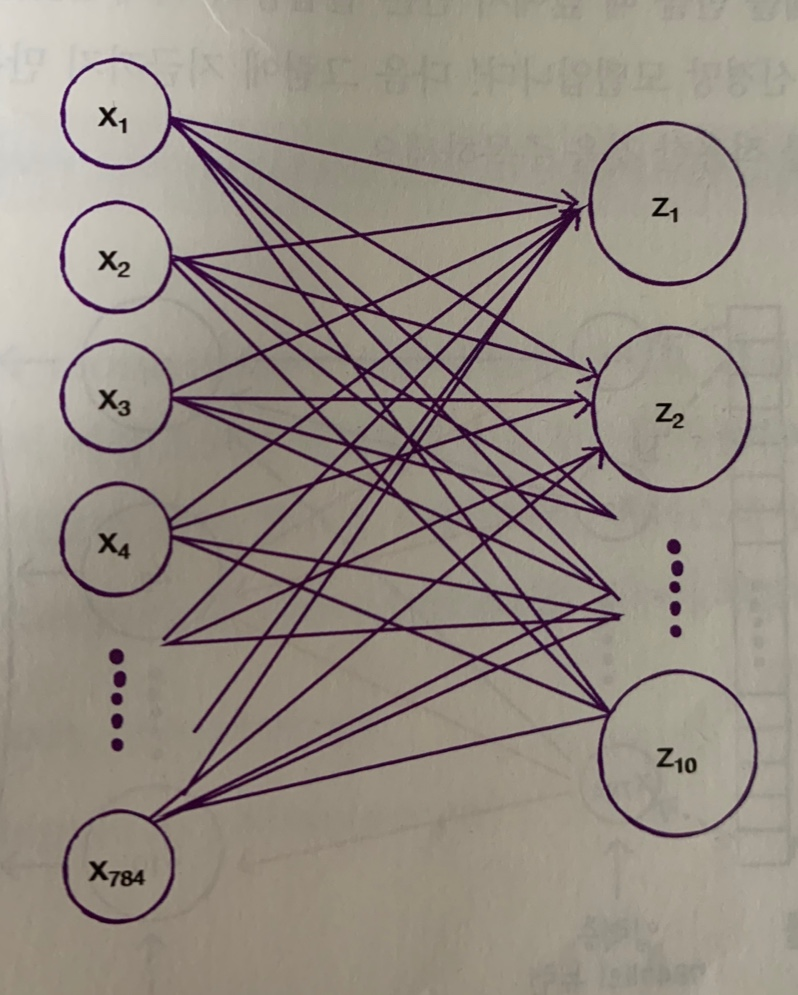
그림처럼 왼쪽의 784개의 픽셀과 10개의 뉴런이 모두 연결시켜보면 784x10=7840개의 연결된 선을 볼 수 있다
빽빽하다고 해서 밀집층이라고 부르는 것이다.
또는, 양쪽 뉴런(x와 z)이 모두 연결되어 있어서 완전 연결층(fully connected layer)라고 부른다
dense = keras.layers.Dense(10, activation='softmax', input_shape=(784,))케라스의 Dense 클래스를 사용해 밀집층을 만들어보자
- 10은 뉴런의 개수(z를 말하는 것)
- activation은 뉴런의 출력에 적용할 함수(아까 본 선형 방정식을 의미하는 것. 이 선형 방정식에는 소프트맥스, 시그모이드 등 다양한 종류가 있음)
- input_shape는 입력의 크기이다. 즉, x를 의미한다고 봐도 무방하다.
위와 같이 신경망 층을 만들었다!

여기서 소프트맥스(softmax) 함수가 뭘까?
소프트맥스 함수는 확률의 총합이 1로 나타내주는 것으로, 어떤 분류에 속할 확률이 제일 높을지 쉽게 예상할 수 있다.
예를 들어, 어떤 사진을 보고 사과, 바나나, 자두인지 구분한다고 생각해보자. 이때 소프트맥스 함수를 써서(다른 추가적인 알고리즘도 필요하겠지만,, 예시로) 사과에 속할 확률이 1이라고 했을 때 어떤 이미지가 0.8정도 된다면 이는 사과라고 할 수 있다는 의미이다.
model = keras.Sequential(dense)위와 같은 문장으로 아까 만든 밀집층을 가진 인공 신경망 모델!을 만들었다
(여기서 추가적인 개념들이 필요한데, 너무 어려우니 생략...)
model.fit(train_scaled, train_target, epochs=5)위와 같이 모델을 훈련을 시켜봤다
epochs는 전체 모델을 5번 돌려본다는 의미!
Epoch 1/5
1500/1500 [==============================] - 6s 2ms/step - loss: 0.6065 - accuracy: 0.7952
Epoch 2/5
1500/1500 [==============================] - 3s 2ms/step - loss: 0.4774 - accuracy: 0.8397
Epoch 3/5
1500/1500 [==============================] - 3s 2ms/step - loss: 0.4566 - accuracy: 0.8469
Epoch 4/5
1500/1500 [==============================] - 3s 2ms/step - loss: 0.4441 - accuracy: 0.8525
Epoch 5/5
1500/1500 [==============================] - 3s 2ms/step - loss: 0.4366 - accuracy: 0.8546그럼 모델이 5번 훈련되는 동안 손실값과 정확도를 볼 수 있다.
모델을 훈련시킬수록 정확도가 높아진다는 것을 알 수 있다
model.evaluate(val_scaled, val_target)그럼 이 모델이 얼만큼의 성능을 내는지 아까 덜어낸 검증 세트로 평가를 해보자
375/375 [==============================] - 1s 2ms/step - loss: 0.4571 - accuracy: 0.8478
[0.45714762806892395, 0.8477500081062317]그러면 훈련세트보다 조금 낮은 약 84%의 정확도가 나왔음을 볼 수 있다.
이번엔 심층 신경망
from tensorflow import keras
(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()케라스에서 데이터셋을 불러들였다
from sklearn.model_selection import train_test_split
train_scaled = train_input / 255.0
train_scaled = train_scaled.reshape(-1, 28*28)
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state=42)그리고 계속 하던 것처럼 훈련세트(train_scaled, train_target)와 검증세트(val_scaled, val_target)로 나누었다
이제 우리는 인공신경망 모델에 2개의 층을 추가해볼 것이다.

입력층과 출력층 사이에 밀집층이 추가되었는데 입력층과 출력층 사이에 있는 모든 층을 은닉층(hidden layer)라고 부른다
dense1 = keras.layers.Dense(100, activation='sigmoid', input_shape=(784,)) #은닉층
dense2 = keras.layers.Dense(10, activation='softmax') #출력층dense1은 은닉층이고, dense2는 출력층이다
dense1은 100개의 뉴런을 가진 밀집층(dense)이고, 시그모이드 함수(아까 본 활성화함수 중 한 종류)를 사용했다
dense2는 클래스를 분류(softmax함수가 '분류'하는 거)하기 때문에 10개의 뉴런을 두었다
model = keras.Sequential([dense1, dense2])아까처럼 층을 만들었으니 모델!을 만든다. dense1과 dense2를 추가해 심층 신경망을 만들었다
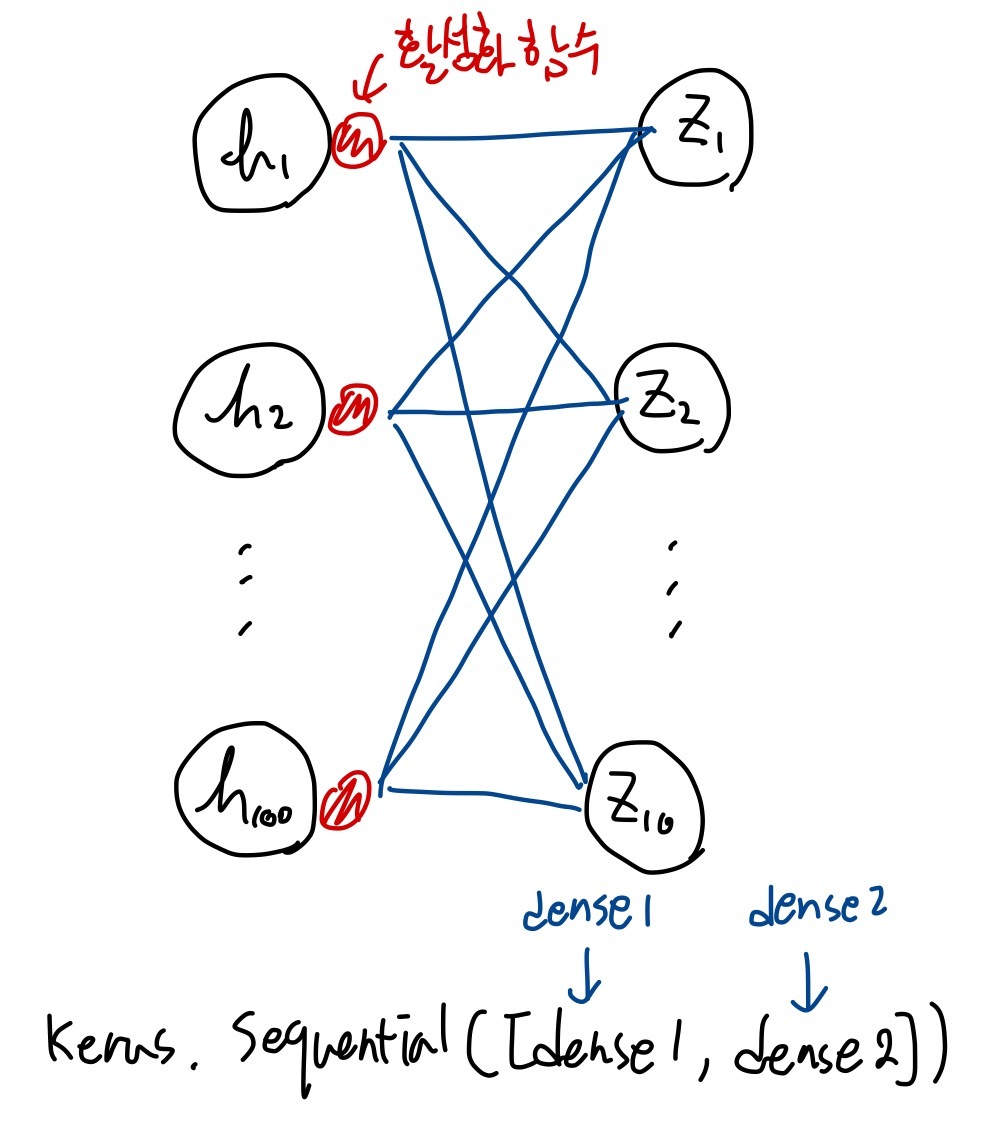
이런 식으로
model.summary()모델이 어떻게 만들어졌는지, 각 층의 이름이 무엇이며, 몇 개의 입력값과 출력값이 들어가있는지 요약해서 볼 수 있다
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 100) 78500
_________________________________________________________________
dense_2 (Dense) (None, 10) 1010
=================================================================
Total params: 79,510
Trainable params: 79,510
Non-trainable params: 0
_________________________________________________________________Param 매개변수는 각 층(은닉층, 출력층, 입력층 등)에 있는 가중치, 절편, 모델 파라미터 개수를 나타낸다
은닉층(dense_1)의 파라미터 개수를 살펴보자
입력층에 784개의 뉴런(픽셀 하나인 x를 의미)이 있고, 은닉층에는 100개의 뉴런이 있다. 가충치의 개수가 784x100개 이고 100개의 뉴런은 100개의 절편이 있다. 이를 다 더하면 78500개가 나온다.
그럼 출력층(dense_2)의 파라미터 개수를 살펴볼까
출력층의 파라미터 개수는 은닉층에 100개의 뉴런이 있고 출력층에 10개의 뉴런이 있어서, 가중치는 100x10개이고 절편은 10개가 있어서 1010개의 가중치가 있음을 볼 수 있다
이제 모델을 훈련시켜보자
model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
model.fit(train_scaled, train_target, epochs=5)이번에도 epochs를 5로 주어서 5번동안 훈려시키게끔 만들었다
Epoch 1/5
1500/1500 [==============================] - 4s 3ms/step - loss: 0.5662 - accuracy: 0.8066
Epoch 2/5
1500/1500 [==============================] - 4s 3ms/step - loss: 0.4110 - accuracy: 0.8519
Epoch 3/5
1500/1500 [==============================] - 4s 3ms/step - loss: 0.3772 - accuracy: 0.8631
Epoch 4/5
1500/1500 [==============================] - 4s 3ms/step - loss: 0.3546 - accuracy: 0.8705
Epoch 5/5
1500/1500 [==============================] - 4s 3ms/step - loss: 0.3372 - accuracy: 0.8775이렇게 은닉층을 추가하니까 아까보다 훨씬 더 정확도가 잘 나왔음을 볼 수 있다
84%에서 87%로 정확도가 늘어났다
신경망 모델 구현
이번엔 손실값을 줄일 수 있는 방법에 대해서 살펴보자
- 손실곡선
손실? 손실함수! 머신러닝이나 딥러닝 모델의 출력값과 사용자가 원하는 출력값의 오차를 의미한다.
손실값이 낮아질수록 더 성능이 좋은 모델이라고 볼 수 있다
model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
history = model.fit(train_scaled, train_target, epochs=5, verbose=0)
print(history.history.keys())
dict_keys(['loss', 'accuracy'])모델을 훈련시켜서(아까 본 모델) 손실값(loss)와 정확도(accuracy)에 대해서 알아보자
import matplotlib.pyplot as plt
plt.plot(history.history['loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()에포크를 이용해 몇 번 모델을 훈련시킬수록 손실값이 낮아지는지 그래프로 살펴보자

에포크가 증가할수록 손실값이 작아져서 훈련이 잘 되고 있음을 볼 수 있다
plt.plot(history.history['accuracy'])
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()이번엔 같은 방법으로 정확도를 살펴보자
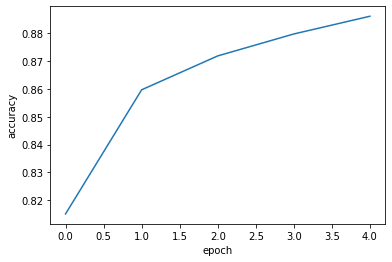
에포크가 증가할수록(훈련을 많이 시킬수록) 정확도가 높아지는 것을 볼 수 있다
model = model_fn()
model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
history = model.fit(train_scaled, train_target, epochs=20, verbose=0)
plt.plot(history.history['loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()이번엔 에포크를 20으로 증가시켜 훈련시켜보고 그래프를 그려보자

여전히 손실값이 줄어듦을 볼 수 있다 -> 즉, '훈련세트에 맞는' 모델이 만들어지고 있는 것이다.
하지만 이게 좋지만은 않다
왜냐면, 훈련세트에 잘 맞는 모델을 만들면 좋지만 실전에 투입했을 때 새로운 데이터에 일반화 되지 못하는 경향이 있다.
그래서 검증세트나 테스트세트에서 적절한 일반화 성능을 얻을 수 있어야한다
model = model_fn()
model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')
history = model.fit(train_scaled, train_target, epochs=20, verbose=0, validation_data=(val_scaled, val_target))케라스에서 검증손실을 자동으로 계산해주는 validation_data를 사용하여 각 에포크마다 훈련 손실과 정확도를 함께 계산해보자
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()훈련세트의 손실값과 검증세트의 손실값을 출력해보자

훈련세트는 에포크가 증가함에 따라 손실값은 감소하지만,
검증세트는 초반에는 좋아진듯 보이나 후반으로 갈수록 손실값이 커지고 있음을 볼 수 있다
즉, 이 모델은 훈련세트에는 잘 맞지만 검증세트에는 잘 맞지 않는 과대적합된 모델이라고 볼 수 있다
여기서 잠깐, 과대적합이 뭐지?
위처럼 훈련세트에서 훈련했을 때 점수가 좋았는데, 테스트세트나 검증세트에서 점수가 나쁘다면 모델이 훈련세트에 과대적합(overfitting) 되었다고 말한다. 즉, 훈련세트에만 잘 맞는 모델이라 테스트 세트와 나중에 실전에 투입하여 새로운 데이터를 만났을 때 제대로 동작하지 않을 것이라는 의미이다!
이와 반대로 훈련세트보다 테스트세트의 점수가 높거나 모두 너무 낮은 경우에는 어떨까?
이런 경우에는 모델이 훈련세트에 과소적합(underfitting) 되었다고 말한다. 즉, 모델이 너무 단순해서 훈련세트에 적절히 훈련되지 않은 경우이다.

그래서 과소적합과 과대적합을 막기 위해 우리는 모델의 최적점을 찾아야한다!
드롭아웃(dropout) : 신경망 모델에만 있는 규제 방법
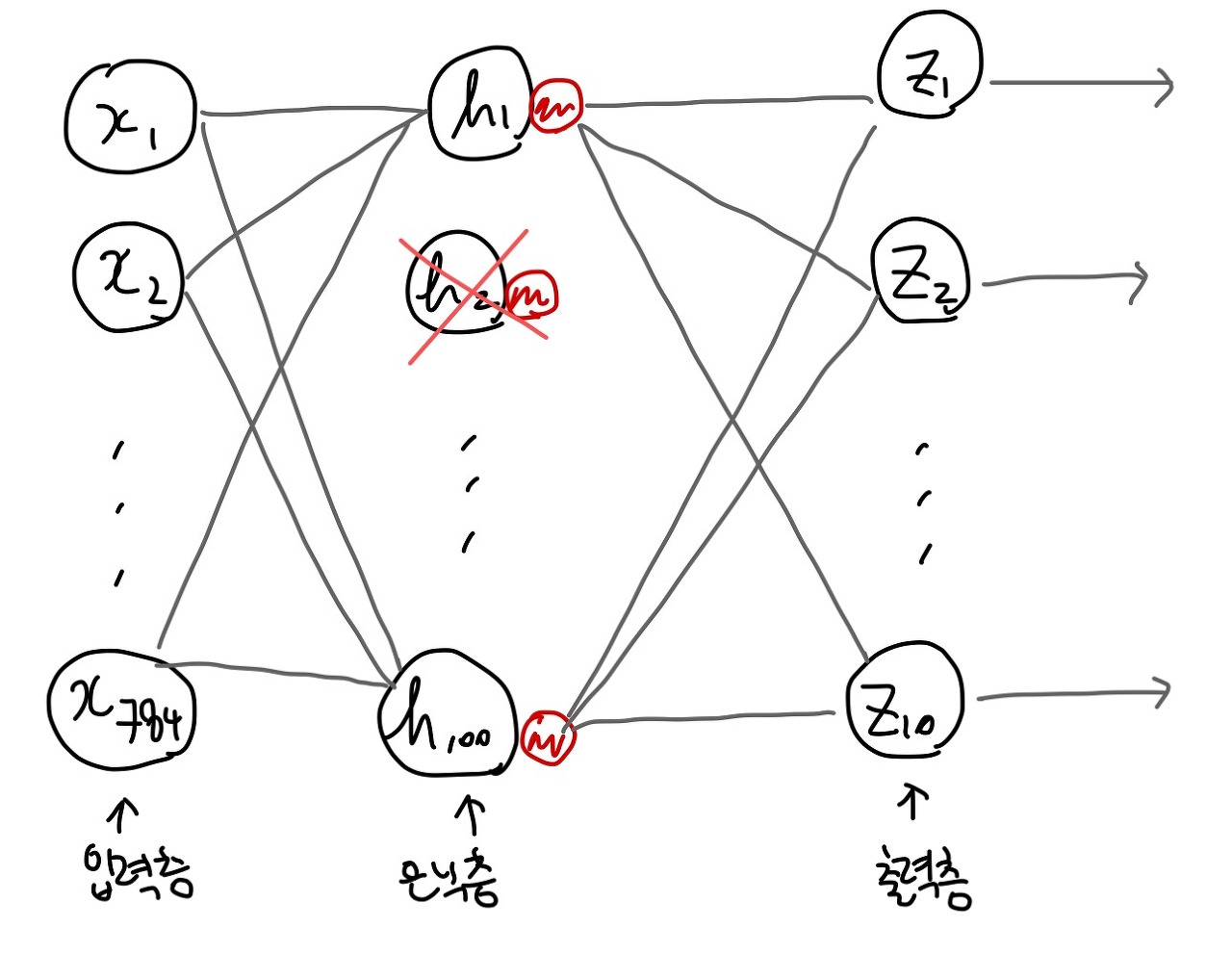
은닉층의 h2를 껐다고 보면된다
즉, 훈련할 때만 임의로 은닉층의 뉴런 하나가 없는 것처럼 계산하는 것이다
이러면 뉴런이 훈련세트에 잘 맞지 않게 되어 어떤 특정 뉴런에 과도하게 의존하는 현상을 막을 수 있다.
드롭아웃은 keras.layers.Dropout이라고 특정 층이 제공된다. 은닉층-밀집층 다음에 드롭아웃층을 추가하면 은닉층의 뉴런 계산 일부가 되지 않는다
model = model_fn(keras.layers.Dropout(0.3))
model.summary()100개의 은닉층의 뉴런중 30개가 계산이 안되도록 드롭아웃시켰다
Model: "sequential_8"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_5 (Flatten) (None, 784) 0
_________________________________________________________________
dense_15 (Dense) (None, 100) 78500
_________________________________________________________________
dropout (Dropout) (None, 100) 0
_________________________________________________________________
dense_16 (Dense) (None, 10) 1010
=================================================================
Total params: 79,510
Trainable params: 79,510
Non-trainable params: 0
_________________________________________________________________드롭아웃은 '훈련할 때만' 계산을 '끄는' 용도이기 때문에 밀집층과 출력층의 크기는 전과 같다
드롭아웃은 학습되는 데이터가 없어 모델 파라미터 개수가 0이다
model.compile(optimizer = 'adam',loss='sparse_categorical_crossentropy', metrics='accuracy')
history = model.fit(train_scaled, train_target, epochs=20, verbose=0, validation_data=(val_scaled, val_target))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()훈련세트와 검증세트의 손실값을 알아보면
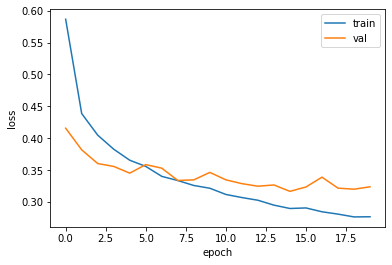
이렇게 에포크가 증가할수록 손실값이 훈련세트의 손실을 잘 따라가고 있음을 볼 수 있다.
즉, 너무 급격하게 검증세트의 손실값이 올라가고 있지 않다!
끗! 고생하셨습니다
'머신러닝 + 딥러닝' 카테고리의 다른 글
| 딥러닝 : 이미지를 위한 인공 신경망 (0) | 2022.07.19 |
|---|---|
| 머신러닝 | 딥러닝 (0) | 2022.07.06 |
| [혼공딥] CHAPTER 09-1 순차 데이터와 순환 신경망 (0) | 2022.01.04 |
| [혼공딥] CHAPTER 08-3 합성곱 신경망의 시각화 (0) | 2022.01.04 |
| [혼공딥] CHAPTER 08-2 합성곱 신경망을 사용한 이미지 분류 (1) | 2022.01.04 |



